1. Introduction
A matrix is a rectangular array of numbers or functions arranged in rows and columns. The concept of matrices is fundamental in various fields such as mathematics, physics, engineering, computer science, and economics. Matrices are used to solve systems of linear equations, perform linear transformations, and represent data or relations.
The plural of “matrix” is matrices. Mathematically, a matrix is often denoted by uppercase letters (e.g., A, B, C), and its elements are arranged in rows and columns.
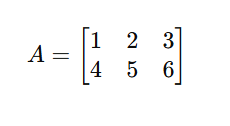
This is a 2×3 (2 rows, 3 columns) matrix.
2. Notation and Terminology
Order of a matrix: Number of rows × number of columns. If matrix A has m rows and n columns, it’s called an m × n matrix.Element of a matrix: Denoted as aija_{ij}aij, the element at the ith row and jth column.
Square matrix: A matrix with an equal number of rows and columns (n × n).
Rectangular matrix: A matrix where the number of rows ≠ number of columns.
3. Types of Matrices
a. Row Matrix
A matrix that has only one row. A row matrix is a matrix that consists of only one row. It can have multiple columns, but the number of rows must be exactly one. For example, a matrix like [3 5 7] is a row matrix because it has only one horizontal line of elements. These are useful when representing data in a single-dimensional array format.
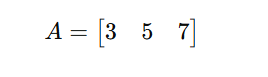
b. Column Matrix
A matrix that has only one column.
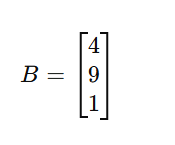
c. Square Matrix
A matrix with the same number of rows and columns.
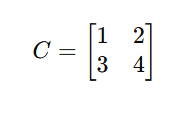
d. Zero Matrix (Null Matrix)
A matrix in which all elements are zero.
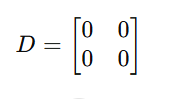
e. Diagonal Matrix
A square matrix where all non-diagonal elements are zero.
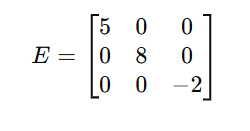
f. Scalar Matrix
A diagonal matrix where all diagonal elements are equal.
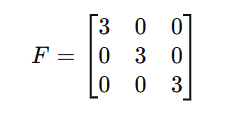
g. Identity Matrix (Unit Matrix)
A square matrix with 1s on the diagonal and 0s elsewhere.
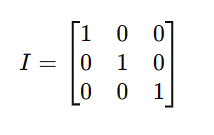
h. Upper Triangular Matrix
A square matrix where all elements below the main diagonal are zero.
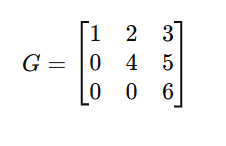
i. Lower Triangular Matrix
A square matrix where all elements above the main diagonal are zero.
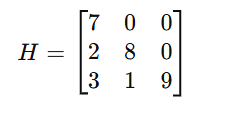
j. Symmetric Matrix
A square matrix that is equal to its transpose,
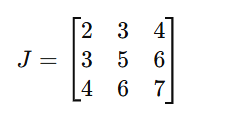
k. Skew-Symmetric Matrix
A square matrix that satisfies A=−ATA = -A^TA=−AT, and diagonal elements are zero.
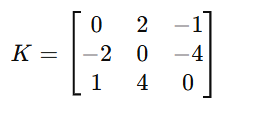
l. Orthogonal Matrix
A square matrix whose transpose is equal to its inverse, i.e., ATA=IA^T A = IATA=I.
m. Singular Matrix
A square matrix with determinant zero. It is non-invertible.
n. Non-Singular Matrix
A square matrix with a non-zero determinant. It is invertible.
o. Sparse Matrix
A matrix in which most of the elements are zero.
p. Dense Matrix
A matrix in which most of the elements are non-zero.
Leave a Reply